T-toetsen
Hoeveel vrijheidsgraden horen daarbij?
Er zijn verschillende t-toetsen. Zo is er bijvoorbeeld de t-toets voor één gemiddelde (one-sample t-test) en de t-toets voor het verschil in gemiddelde van twee onafhankelijke groepen (independent samples t-test). Voor de meeste t-toetsen kan het juist aantal vrijheidsgraden vrij eenvoudig worden uitgerekend. Maar, het is zeker niet voor elke t-toets: n-1 !
Om in een t-toets het juiste significantieniveau (dwz, de p-waarde) te kunnen bepalen, moet je weten welke T-verdeling van toepassing is voor die toets. In tegenstelling tot de standaardnormaalverdeling, waarvan er slechts één is, zijn er in principe oneindig veel verschillende T-verdelingen. Die T-verdelingen lijken allen zeer sterk op elkaar (Zie Figuur 1), maar zijn toch net wat anders van vorm en dat is met name zo in de staarten van de verdelingen.
Om de juiste p-waarde te bepalen moet je weten welke T-verdeling van toepassing is. Zonder verder op de wiskundige achtergrond in te gaan: de verschillende T-verdelingen worden aangegeven met "vrijheidsgraden" (degrees of freedom). Een T-verdeling met 10 vrijheidsgraden is bijvoorbeeld dus net wat anders van vorm dan een T-verdeling met 25 vrijheidsgraden en zal voor dezelfde t-waarde dus toch net een iets andere p-waarde opleveren. In Figuur 1 (boven) zijn drie verdelingen weergegeven: de T-verdelingen met 10 en 25 vrijheidsgraden en de normaalverdeling. In Figuur 1 (onder) is de linkerzijde van de Figuur 1(boven) uitvergroot. Er is uitgetekend voor de linkszijdige p-waarde voor een T van -2.0, dus verschillende p-waarden oplevert voor de verschillende verdelingen. Met minder vrijheidsgraden zal de p-waarde wat groter zijn dan met met meer vrijheidsgraden. Dat is ook zo voor rechts- en tweezijdige p-waarden. Een hogere p-waarde betekent altijd: "minder significant". Of te wel, met minder vrijheidsgraden wordt de t-waarde dus net wat minder significant! Het aantal vrijheidsgraden is dus wel belangrijk.
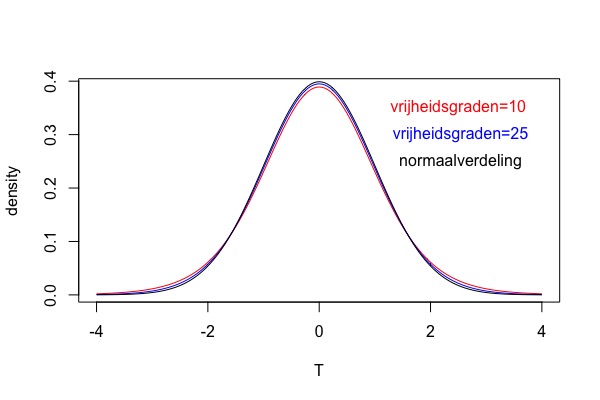
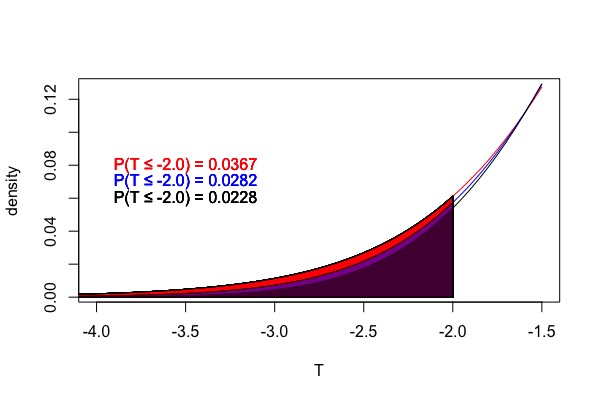
Figuur 1. boven: T-verdelingen voor 10 en 25 vrijheidsgraden en de standaardnortmaalverdeling. Onder: detail van de linkerstaarten van de T-verdelingen
Voor de meest voorkomende t-toetsen zijn de juiste aantallen vrijheidsgraden in Tabel 1 samengevat:
| Toets | Vrijheidsgraden | Toelichting |
|---|---|---|
| One sample t-test | \[n-1\] | De steekproefgrootte min één |
| Paired-samples t-test | \[n-1\] | Het aantal paren min één |
| Independent samples t-test (equal variances assumed) |
\[n_1 + n_2 - 2\] | de grootte van de eerste groep plus de grootte van de tweede groep, min twee |
| Independent samples t-test (equal variances NOT assumed) |
\[Sattertwaithe\] | Het aantal vrijheidsgraden hangt af van de grootte van beide groepen èn van de variantie van beide groepen. Minimaal bedraagt het aantal: 'kleinste groep - 1' en maximaal 'n1+n2 -2'. |
| t-toets voor een correlatiecoefficient | \[n-2\] | De steekproefgrootte min twee |
| t-toets voor een regressiecoefficient | \[n-p-1\] | De steekproefgrootte min het aantal predictoren min 1 |
De T-toets voor onafhankelijke groepen
De grootste verwarring onstaat echter meestal in de t-toets voor onafhankelijke groepen. Ten eerste is het verwarrend dat er twee varianten bestaan van deze toets die sowieso al een verschillend aantal vrijheidsgraden hebben. Wellicht was je dat ook al opgevallen in Tabel 1, of in de output van SPSS bijvoorbeeld. Ten tweede wordt het verwarrend omdat voor één van die twee varianten eigenlijk een lastige berekening gemaakt moet worden (de Sattertwaithe benadering), waarvoor in plaats echter vaak een makkelijkere maar niettemin onjuiste rekenregel wordt gehanteerd. Hoe zit dat?
De eerste variant van de independent samples t-test is de zogenaamde Student T-toets. Deze variant wordt ook wel de "gepoolde" t-toets genoemd. Deze variant maakt in de berekening van de t-waarde een aanname dat de populatievariantie in de ene groep even groot is als in de andere groep. Voor deze variant van de t-toets is het aantal vrijheidsgraden makkelijk te bepalen. Zie Tabel 1.
De tweede variant van de t-toets voor onafhankelijke groepen is de Welch T-toets, of te wel de 'niet-gepoolde' of 'equal variances NOT assumed' variant. Deze variant heeft vaak de voorkeur boven de Student T-toets omdat er geen aanname over de gelijkheid van varianties wordt gemaakt. Het aantal vrijheidsgraden is voor deze toets echter niet heel makkelijk te bepalen omdat dat afhangt van zowel de beide groepsgroottes als van de varianties binnen beide groepen. Het juiste aantal vrijheidsgraden kan worden uitgerekend met de zogenaamde 'Sattertwaithe benadering'. De naam zegt het misschien al, ook dit is niet exact juist, maar dat is echt verwaarloosbaar. Deze benadering geeft verreweg de beste schatting vergeleken met alle andere regels.
De Sattertwaithe benadering is eerlijk gezegd een formule die best lastig zonder fouten met de hand is uit te rekenen. Ik probeer dat zelf ook veel mogelijk te vermijden want het is heel foutgevoelig, kost veel te veel tijd, en er is toch een prima online calculator beschikbaar. In vergelijking 1 staat voor de volledigheid de formule voor de Sattertwaithe benadering, maar wij raden dus aan om de Sattertwaithe calculator te gebruiken. Als ik het zelf toch zo nodig met een rekenmachientje moet uitrekenen, houd ik altijd in gedachte dat de uitkomst altijd tussen 'de grootte van de kleinste groep, min één' en 'de som van beide groepsgroottes, min twee' moet liggen: Dat is een makelijke manier om de uitkomst te controleren. Het is niet waterdicht nauurlijk, maar hoger of lager is zeker fout!
Vergelijking 1). Vrijheidsgraden volgens de Sattertwaithe benadering. \[vrijheidsgraden = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2} {\frac{1}{n_1-1}(\frac{s_1^2}{n_1})^2 + \frac{1}{n_2-1}(\frac{s_2^2}{n_2})^2 } \]
Omdat de Sattertwaith benadering dus lastig handmatig is uit te rekenen, wordt in plaats daarvan in de statistiekboeken vaak een 'handige' rekenregel gehanteerd, namelijk: ' Het aantal vrijheidsgraden is gelijk aan grootte van de kleinste groep min één'. Deze regel is echter niet correct. De boeken geven dat meestal ook gewoon toe, maar de ervaring leert dat daar vaak wat te snel overheen gelezen wordt. De handige rekenregel geeft eigenlijk vrijwel altijd een te laag aantal vrijheisdsgraden, met als gevolg dat p-waardes vaak net iets te hoog worden geschat. In eufemistische termen wordt de toets dan "iets te conservatief" genoemd. Dit is een verwarrende regel die we eigenlijk niet meer zouden moeten willen gebruiken want eigenlijk is er tegenwoordig ook niet zo veel reden meer om die handige rekenregel te gebruiken; computers maken immers korte metten met Sattertwaithe. Alle statistiekprogramma's kunnen dat. Als je handmatig of met een rekenmachine deze toets doet, gebruik dan gewoon onze Sattertwaithe calculator om het juiste aantal vrijheidsgraden te bepalen.
Vaak krijg je volgens de Sattertwaithe benadering een aantal vrijheidsgraden met decimalen. Dit kun je niet goed opzoeken in een tabellenboek want dat staat er waarschijnlijk niet in. Er is geen enkel tabellenboek groot genoeg om alle mogelijke T-verdelingen in op te nemen. Maar geen nood, ook hier hebben we een calculator voor: de 'van T naar p' calculator.
Voor studenten is het interessant om zich te realiseren dat het aantal vrijheidsgraden voor een docent altijd problemen geeft bij het maken van tentamenvragen over t-toetsen voor twee onafhankleijke groepen. Het gaat immers wat ver om studenten het aantal vrijheidsgaden volgens Sattertwaithe te laten uitrekenen met een rekenmachine , en het aantal vrijheidsgraden komt vrijwel altijd veel te onhandig uit om de p-waarde in een tabel, zoals dat in het cursusboek stond, op te zoeken. Dat kan alleen maar een hoop rekenfouten opleveren dat eigenlijk niet de kennis van de student weergeeft: niet zo'n beste vraag dus. Misschien zegt de docent in de vraag dus, tegen beter weten in, wel "gebruik de rekenregel 'kleinste n -1'", of 'de rekenregel uit het boek', of mischien wordt in de vraag niet gevraagd om zowel de t- als de p-waarde. Sommige docenten zullen wellicht in plaats van de Welch T-toets, de gepoolde t-toets (Student's T-test) bevragen omdat de vrijheidsgraden daar wel makkelijk voor zijn te bepalen (in de vraag zal dan zo iets staan als: "ga er vanuit dat de populatievarianties van beide groepen gelijk zijn aan elkaar").
Tot slot een kort punt van aandacht bij het rapporteren van de independent samples t-test. Volgens de APA regels wordt het aantal vrijheidsgraden tussen haakjes gezet. Bijvoorbeeld: " t(99) =3.28; p = .0014". In dit voorbeeld zijn er dus 99 vrijheidsgraden en is de t-waarde 3.28 met een bijbehorende p-waarde van 0.0014. Een veel voorkomende fout is dat voor het aantal vrijheidsgraden 'kleinste groep -1' wordt gerapporteerd, terwijl de p-waarde is bepaald voor een T-verdeling waarbij het aantal vrijheidsgraden is uitgerekend met de Sattertwaithe benadering (bv omdat die uitkomst uit spss kwam). De p en T waarden passen dan natuurlijk niet meer bij elkaar. Als de Sattertwaith benadering (voorkeur) wordt gebruikt, rapporteer dan daarvan ook de vrijheidsgraden. SPSS rapporteert overigens in de output tabel van de independent samples t-toets ook gewoon het aantal vrijheidsgraden volgens Sattertwaithe. Als je eigenwijs bent en toch de rekenregel gebruikt voor het bepalen van de p-waarde, rapporteer dan wel de vrijheidsgraden volgens de rekenregel natuurlijk.
