Standaarddeviaties

Populatie vs steekproef

Eén van de eerste dingen die een beginnend onderzoeker tegen komt in de statistiekboeken is de standaarddeviatie en variantie. En dan dan begint de verwarring. Er blijken namelijk twee verschillende formules voor de standaarddeviatie (Eq 1 en Eq 2) te bestaan:

Eq 1. \(\sigma = \sqrt{\Sigma\frac{(x_i -\mu)^2}{n} } \)

Eq 2. \(s = \sqrt{\Sigma\frac{(x_i -\bar{x})^2}{n-1} } \)

Wat is het verschil, waarom staat nu in de eerste formule n en in de tweede n-1, en wanneer gebruik je nu eigenlijk welke?

Het korte antwoord is redelijk makkelijk, namelijk: Als de hele populatie is gemeten (en weet je dus het populatiegemiddelde \( \mu \)), dan wordt de eerste formule gebruikt om de populatiestandaarddeviatie \( \sigma\) te berekenen. Als er een steekproef is gemeten, en alleen het steekproefgemiddelde \( \bar{x} \) dus bekend is, dan wordt de tweede formule gebruikt om een zo goed mogelijk schatting, \( s \), van de standaarddeviatie van de populatie te maken waar de steekproef uit afkomstig was. Als de formule in Eq 1 toch zou worden gebruikt op een steekproef (en je zou alleen \( \mu \) vervangen door \( \bar{x} \) , dan blijkt die schatting van de standaarddeviatie van de populatie eigenlijk altijd te klein te zijn, fout dus.

Het lange antwoord is wat lastiger. In deze lecture note gaan we dieper in op wat de standaarddeviatie precies is en laten we middels een computersimulatie zien dat de formule voor de standaarddeviatie van een populatie niet zomaar kan worden toegepast op een steekproef. We zullen daarvoor een aantal wellicht nieuw begrippen gebruiken, namelijk verwachte waarde, zuivere schatters, en bias. Deze lecture note wordt afgesloten met een stukje algebra voor de liefhebber

Wat is de standaarddeviatie?

De standaarddeviatie is een getal dat aangeeft hoe ver de (meet)waarden uit elkaar liggen. Of te wel, hoe groot is de spreiding? Er zijn veel verschillende maten om aan te geven hoe groot de spreiding is, net zoals er ook meerdere maten zijn om het centrum van de meetwaarden aan te duiden (gemiddelde, mediaan, modus, etc). De interkwartielafstand, de variantie of het bereik zijn voorbeelden van zulke spreidingsmaten. Vaak wordt echter gekozen voor de standaarddeviatie. Het is een handige maat die veel inzicht geeft in hoeveel de data gespreid is èn waar relatief makkelijk mee door te rekenen is. Veel van de toetsen en betrouwbaarheidsintervallen die in statistiekcursussen worden behandeld, maken op een of andere manier gebruik van standaarddeviaties.

De gedachte achter de standaarddeviatie is dat het aangeeft aan hoe ver de meetwaarden gemiddeld afwijken van het gemiddelde van die meetwaarden. De verschillen tussen de meetwaarden en het gemiddelde noemen we in de statistiek ook wel deviaties. Het gemiddelde van de deviaties lijkt op het eerste gezicht best een goede maat voor de spreiding, maar is dat toch niet. Dat zit zo: Deviaties zijn positief als de meetwaarden boven het gemiddelde ligt en negatief als het er onder ligt. Het gemiddelde van de deviaties is per definitie gelijk aan 0, want er ligt net zoveel boven (positief) het gemiddelde als er onder (negatief).

Een relatief eenvoudige oplossing is om alle deviaties eerst te kwadrateren om ze positief te maken en vervolgens daarvan het gemiddelde uit te rekenen. Dit is wat we noemen de variantie. Als we de wortel trekken uit de variantie komen we uit op de standaarddeviatie. Dit is de definitie van de standaarddeviatie: de wortel uit het gemiddelde van de gekwadrateerde deviaties. Het is wiskundig niet precies gelijk aan de gemiddelde deviatie, maar lijkt er wel sterk op. Deze definite staat in Eq 1. De Griekse kleine letter sigma, \( \sigma \), is het symbool voor de standaarddeviatie, de Griekse hoofdletter (sigma) \( \Sigma \) geeft aan dat gekwadrateerde deviaties moeten worden opgeteld. \( \Sigma \) staat dus voor "Som". \( \mu \) is het gemiddelde van alle waardes \( x_i \) , en n is het aantal waardes.

Verwachte waarde en Bias

Als een relatief kleine random steekproef getrokken wordt uit een grote populatie mag je verwachten dat de statistieken van de steekproef ongeveer overeenkomen met de parameters van de populatie. Dat wil zeggen, het gemiddelde, de mediaan, de standaarddeviatie etc van de steekproef zal ongeveer overeen moeten komen met respectievelijk het gemiddelde, de median en de standaarddeviatie van de populatie. Anders zou het immers geen zin hebben om een steekproef te trekken, niet waar?

Soms geeft de steekproef een te grote schatting van het populatiegemiddelde, soms te klein, maar wanneer heel veel steekproeven genomen zouden worden zou, gemiddeld genomen over al die steekproeven, het steekproefgemiddelde overeen moeten komen met het populatiegemiddelde. We noemen het gemiddelde van alle mogelijke steekproefgemiddelden de verwachte waarde van de het steekproefgemiddelde. Zo is er ook een verwachte waarde voor de mediaan, de standaarddeviatie, etc.

In het geval van het gemiddelde kan wiskundig worden bewezen dat de verwachte waarde van het steekproefgemiddelde overeenkomt met het populatiegemiddelde. Dat betekent dat, hoewel een steekproefgemiddelde per steekproef mischien wel hoger of later uit is gepakt dan het populatiegemiddelde, het steekproefgemiddelde niet systematisch hoger of lager is. We noemen het steekproefgemiddelde daarom ook wel een zuivere schatter voor het populatiegemiddelde, dus zonder bias.

Hoewel dit klopt voor het gemiddelde, klopt dat niet voor andere statistieken zoals de standaarddeviatie en de variantie. In de formule in Eq. 1 kan niet zomaar \( \mu \) vervangen worden door \( \bar{x}\), want dan is het resultaat géén zuivere schatting van de populatiestandaarddeviatie, maar blijkt systematisch te klein te zijn! Met andere woorden, het zou een bias hebben.

Simulatie I

Eén van de mooie dingen van een computer is dat het dezelfde taak, heel vaak en heel snel achter elkaar kan uitvoeren. Laten we met een computer eens onderzoeken of de verwachte waarde van gemiddelde, standaarddeviatie etc in een steekproef overeenkomen met de populatie. In Figuur 1 is een histogram van een populatie weergegeven. De populatie is zeer groot, Normaal-verdeeld, met een gemiddelde van 100 en een standaarddeviatie van 15 (variantie = 225).

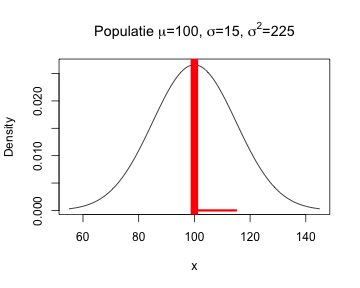
Uit de zeer grote populatie in Figuur 1 zijn 1,000,000 random steekproeven van telkens 10 meetwaarden getrokken. Eén miljoen steekproeven is geen oneindig aantal, maar toch wel heel erg veel, niet waar? Van elk van die één miljoen steekproeven is het gemiddelde, de standaarddeviatie en de variantie volgens Eq 1, waarbij alleen \( \mu \) was vervangen door \( \bar{x} \) berekend. Van deze statistieken zijn vervolgens de gemiddelden over alle steekproeven berekend (dwz de verwachte waardes) en zijn de histogrammen in Figuur 2 gemaakt. de histogrammen voor de standaardeviaties en, meer nog, voor de variantie worden inderdaad enigszins scheef naar rechts. De rode lijnen geven telkens het populatieparameters aan terwijl de gele lijnen het gemiddelde van alle simulaties voorstellen (en zijn bij benadering dus de verwachte waarde). Het verwachte gemiddelde ligt heel dicht bij het populatiegemiddelde, maar de verwachte standaarddeviatie en de verwachte variantie lijkt toch echt te klein. De standaarddeviaties waren gemiddeld ongeveer 7.7% te klein en de verwachte waarde van variantie was zelfs bijna 10% te klein in deze simulatie.

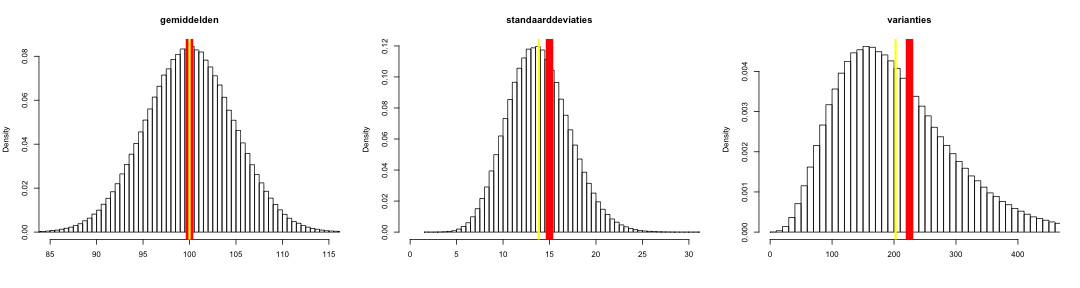
Conceptuele verklaring

De verwachte waarde van de standaarddeviatie in de steekproef heeft dus een bias: hij is te klein. Dit komt omdat in de berekening van de standaarddeviatie in de steekproef de deviaties berekend zijn als het verschil tussen het steekproefgemiddelde en de meetwaarden. Stel nu eens dat een steekproefgemiddelde lager uitvalt dan het populatiegemiddelde, dat kan, maar dat betekent ook dat de steekproef relatief veel waarden uit de lagere regionen van de verdeling had en die dus relatief dicht bij elkaar gelegen hebben. Dat geldt ook voor een steekproefgemiddelde dat hoger uitvalt dan het populatiegemiddelde: relatief veel meetwaarden kwamen dan uit de hogere regionen van de verdeling en die lagen dan dus relatief dicht bij elkaar. Dus, telkens als het steekproefgemiddelde hoger of lager is dan het populatiegemiddelde liggen de meetwaarden dichter bij elkaar dan gemiddeld in de hele populatie het geval is met als gevolg dat de verwachte waarde van de steekproefstandaarddeviatie kleiner is dan standaarddeviatie van de populatie.

De oplossing

Nu blijkt dat er een relatief eenvoudige aanpassing gedaan kan worden in de berekening van de standaarddeviatie waardoor de verwachte waarde wèl (of in elk geval veel beter) overeen komt met de standaarddeviatie in de populatie. Namelijk: De Bessel correctie.

Eq 2. \(s = \sqrt{\Sigma\frac{(x_i -\bar{x})^2}{n-1} } \)

Neem niet de wortel uit het gemiddelde van de gekwadrateerde deviaties (alle deviaties in het kwadraat optellen en delen door het aantal) als standaarddeviatie, maar deel door het aantal waarden min 1. Daar wordt de uitkomst net wat groter door (want je deelt door iets wat net wat kleiner is). Met deze correctie is de standaardeviatie in de steekproef wèl (bijna) een zuivere schatter van de standaarddeviatie in de populatie. De variantie (zonder worteltrekken dus) is helemaal een zuivere schatter. Deze correctie waarbij gedeeld wordt door n-1 ipv n, staat bekend als de Bessel correctie. Eerlijk gezegd moet er wel vermeld worden dat de Bessel correctie wiskundig gezien nog steeds niet helemaal de bias wegneemt in de standaarddeviatie vanwege de wortel in de formule. Voor deze resterende bias in de standaarddeviatie wordt echter meestal niet verder meer gecorrigeerd.

Simulatie II

Simulatie I is nog een keer herhaald, maar dan met de formule uit Eq 2 om de standaarddeviaties en varianties uit te rekenen. De resulaten staan in Figuur 3. Nu blijkt de gele lijn voor de varianties wel mooi midden op de rode lijn te liggen. De verwachte waarde voor de steekproefvariantie lijkt dus nu gelijk te zijn aan de populatievariantie. De verwachte waarde van de standaarddeviatie lijkt echter nog steeds een beetje te klein (ongeveer 2.6%). Maar, dat is wel al een heel stuk beter dan de 7.7% die het eerder was. Gezien de verschillen tussen de steekproeven valt deze resterende bias in het niet en wordt overigens ook nog snel kleiner als er grotere steekproeven genomen zouden worden: Bij een verdubbeling van de steekproef halveert de resterende bias ongeveer.

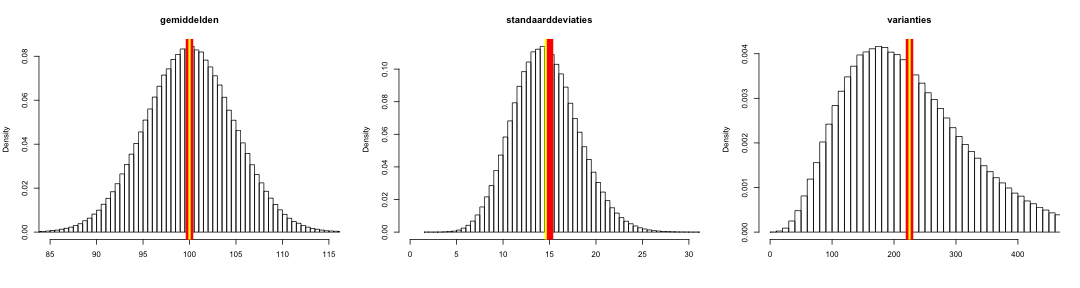
Kritiek

Statistiek is soms een raar vakgebied waarin heel veel formules worden gebruikt, maar bij nadere inspectie een heleboel dingen eigenlijk alleen bij benadering kloppen. Er wordt bijvoorbeeld veel aandacht gegeven aan de Bessel Correctie, die dan toch voor de standaarddeviatie niet helemaal voldoende is. We hebben in de eerdere simulaties in deze lecture note laten zien bij n-1 de standaarddeviatie toch nog steeds net een beetje te klein is; 'n-1.3' zou waarschijnlijk net wat beter werken! Hoe groter de steekproef hoe kleiner de resterende bias en bij kleine steekproeven is de schatting sowieso al erg onnauwkeurig. Dit zijn natuurlijk mooie argumenten om ons niet te druk te maken over de resterende bias. Deze argumenten gelden ook voor de Bessel Correctie, maar de algemene consensus in de statistiekboeken is dat de Bessel correctie gedaan moet worden.

Er is nog een kritiekpunt en dat gaat over welk criterium gebruikt zou moeten worden als argument om de standaarddeviatie te corrigeren met bijvoorbeeld de Bessel Correctie. Vaak wordt de "bias" als criterium gebruikt en dat lijkt heel redelijk. De bias is echt kleiner met een Bessel correctie en verwijnt helemaal bij de variantie. Maar we zouden ook kunnen kijken naar hoever gemiddeld de schatting van sigma afligt met verschillende correcties (dus bias plus random fluctuaties van steekproef tot steekproef) en dan blijkt dat 'n-1' helemaal niet de beste correctie is maar dat 'n - 1' net te klein is voor de standaarddeviatie en voor de variantie is zelfs 'n+1' de betere oplossing.

Dus

Als de bedoeling is dat de standaarddeviatie van de populatie wordt geschat met behulp van een steekproef moet je in de berekening niet delen door n, maar door n-1 zoals in Eq.2, anders is de schatting te klein. We noemen de formule in Eq 2 de steekproefstandaarddeviatie (s). Dit wordt met een Latijnse letter "s" geschreven, om aan te geven dat om schatting van de populatiestandaarddeviatie gaat. Maar als de hele populatie is gemeten, dan is de correctie natuurlijk niet nodig. Wanneer er in de berekening gedeeld is door n, noemen we het de populatiestandaarddeviatie en wordt de Griekse letter sigma, \( \sigma \), gebruikt. Populaties hoeven overigens niet heel groot te zijn; een klas van 20 leerlingen kan ook een hele populatie vormen als de populatie zo gedefineerd is in het onderzoek. Het is dus belangrijk om na te denken over de vraag of de hele populatie gemeten is, of dat er een steekproef uit een populatie is gemeten.

Excel heeft functies voor zowel de populatie- als de steekproefstandaarddeviatie. Met de functies stdev.p en stdev.s kunnen de beide standaarddeviaties respectievelijk worden berekend. Voor de variantie heeft Excel de functies var.p en var.s . Wanneer de standaardeviatie of variantie in R wordt uitgerekend met respectievelijk de functies sd() en var() wordt de "steekproefversie" uitgerekend. In SPSS wordt er ook automatisch van uitgegaan dat de data een steekproef is en geen complete populatie.

Eq 2 geeft een bijna zuivere schatting voor de populatiestandaarddeviatie maar het kwadraat is wel een zuivere schatting van de populatievariantie. Hoewel er nog enkele problemen kleven aan deze definties, is dit wel de breedst geaccepteerde manier in het veld om de standaarddeviatie en de variantie van een populatie te schatten.

---

Appendix

Algebraisch bewijs

Voor de liefhebbers van algebra volgt hieronder nog een (gedeeltelijke) afleiding waaruit blijkt dat de verwachte waarde van de steekproefvariantie inderdaad overeenkomt met de populatievariantie. Als dit niet je ding is, sla het dan gerust over.

Laten we eens uitschrijven wat de verwachte waarde is van de steekproefvariantie. E() staat voor de "Expected value" en is het gemiddelde over alle mogelijke, onafhankelijke realizaties van wat er tussen haakjes staat. E(x) is dus de verwachte waarde van de meetwaarde en zal dus het populatiegemiddelde zijn, terwijl \( E(s^2) \) het gemiddelde over de steekproefstandaarddeviaties van alle steekproeven die uit een populatie kunnen komen. Hier laten we zien dat de verwachte steekproefvariantie zoals geformuleerd in Eq 2. inderdaad overeenkomt met de populatie variantie.

Eerst, drie vergelijkingen over expected values die we verder niet zullen bewijzen:

\[E(x) = \mu \] \[ E(x^2) = \mu^2 + \sigma^2 \] \[ E(\bar{x}^2)= E( x\bar{x})= \mu^2 + \frac{\sigma^2}{n} \]
, met gebruik van deze drie vergelijkingen kan de verwachte waarde van \(s^2\) gevonden worden,

\[ E(s^2) = E ( \frac{\Sigma{(x-\bar{x})^2}}{n-1}) \] \[ = \frac{1}{n-1} E(\Sigma{(x^2 - 2x\bar{x} +\bar{x}^2)} ) \] \[ = \frac{1}{n-1} \Sigma{(E(x^2) - 2E(x\bar{x}) + E(\bar{x}^2))} ) \] \[ = \frac{1}{n-1} \Sigma{(\mu^2 + \sigma^2 - 2(\mu^2 + \frac{\sigma^2}{n}) + \mu^2 + \frac{\sigma^2}{n} } \] \[ = \frac{1}{n-1} {n(\mu^2 +\sigma^2 - 2(\mu^2 + \frac{\sigma^2}{n}) + \mu^2 + \frac{\sigma^2}{n} )} \] \[ = \frac{n}{n-1} {(\sigma^2 - \frac{\sigma^2}{n} )} \] \[ = \frac{n \sigma^2 - \sigma^2}{n-1} \] \[ = \frac{(n-1) \sigma^2 }{n-1} \] \[ = \sigma^2 \]