T-Toetsen

Eén- of tweezijdig?

Bij t-toetsen bestaat er de mogelijkheid om één- of tweezijdig te toetsen. Of beter gezegd, er bestaat de mogelijkheid om links-, rechts- en tweezijdig te toetsen. Ook de niet-parametrische alternatieven voor T-toetsen zoals de Wilcoxon ranksum test kunnen links-, rechts-, en tweezijdig worden uitgevoerd. Bij de meeste andere toetsen, zoals bij een oneway anova is dat niet het geval. 

Eén- en tweezijdig toetsen heeft alles te maken met hoe de hypothese die getoetst wordt, is opgeschreven. In deze lecture note gaan we eerst in op wat hypotheses zijn en waarom er in een t-toets in principe drie verschillende hypotheses kunnen worden gebruikt. Vervolgens zullen we ingaan op hoe de bewijsvoering vóór een alternatieve hypothese in elkaar steekt en wat het begrip overschrijdingskans (p-waarde) daarmee te maken heeft. We zullen daarin ontdekken waarom er met elk van de drie vormen van alternatieve hypotheses een andere p-waarde is geassocieerd.

Wat zijn hypotheses?

Met een steekproef wordt geprobeerd om een uitspraak te doen over de populatie waar de steekproef uit afkomstig was. De populatie is niet geheel gemeten, maar er zou wel een stelling gemaakt kunnen worden over de populatie waarvan we niet zeker weten of het echt zo is.  Bijvoorbeeld: "het populatiegemiddelde is kleiner dan ....". Dit is een stelling over de populatie waarvan we op basis van bijvoorbeeld een theorie vermoeden dat wel eens het geval zou kunnen zijn, maar zeker weten doen we het niet. Deze stelling noemen we de hypothese die getoetst gaat worden. Een hypothese is dus een stelling over de populatie waarvoor wordt geprobeerd te achterhalen of die hypothese ook geloofwaardig is op basis van wat er in een steekproef is gevonden. Dat is op zich best lastig omdat elke steekproef immers net even wat anders zal zijn dan de vorige en de volgende steekproef. Het te kort door de bocht om te zeggen dat als een steekproefgemiddelde lager uitvalt dan je in gedachte had, het populatiegemiddelde dus ook wel kleiner zal zijn dan je gedacht had. Dat kon immers best op toeval zijn berust.

Een onderzoeker vermoedt bijvoorbeeld om diverse redenen dat kinderen op de middelbare school tegenwoordig gemiddeld meer thuis studeren dan vroeger. Vroeger was dat 3 uur per dag en laten we er voor dit voorbeeld vanuit gaan dat we dat met grote zekerheid weten omdat daar vroeger al veel was onderzoek naar gedaan. De onderzoeker vermoedt echter dat kinderen tegenwoordig gemiddeld meer dan dan 3 uur per dag thuis studeren. Dit vermoeden wordt de alternatieve hypothese genoemd en dat wordt vaak aangeduid als \( H_a \). We weten NIET of de alternatieve hypothese klopt. Sterker nog, we zullen nooit helemaal zeker weten of deze hypothese klopt tenzij we de hele populatie gaan doormeten (en dat willen we niet want dat is veel te veel werk).

In een statistische toets wordt vastgesteld hoeveel aanleiding er is om specifiek in deze alternative hypothese te geloven. Of te wel, hoe sterk is het "bewijs" vóór de alternatieve hypothese? Strikt genomen kunnen we niet over bewijs spreken in een statistische toets, want we hebben altijd te maken met een (random) steekproef. Het 'bewijs" is dus nooit sluitend. Dit in het Engels wat makkelijker te formuleren omdat "support" en "evidence" minder sterk zijn dan "proof". In de rest van dit verhaal gebruiken we wel de term "bewijs", met dien verstande dat er geen "wiskundig bewijs" bedoeld wordt, om de tekst zo leesbaar mogelijk te houden. Sommige wetenschappers (en docenten) zijn overigens hooglijk allergisch voor de term "bewijs", dus pas wel een beetje mee op met deze term.

Tegenover de alternatieve hypothese staat de situatie waar tegen het bewijs wordt afgezet. In toetsen wordt dat de nulhypothese genoemd en wordt meestal aangeduid als \( H_0 \) . In ons voorbeeld ligt het voor de hand om het bewijs voor de alternatieve hypothese te zien ten opzichte van de situatie waarin het populatiegemiddelde niet veranderd was ten opzichte van vroeger. Dit is een soort van defaulthypothese: de situatie zoals het de wereld zou moeten zijn als de alternatieve hypothese niet klopt. Default betekent zo iets als standaardwaarde, of standaardinstelling. In de nulhypothese zie je daarom altijd een "=" teken staan. In toetsen zijn we NIET op zoek naar bewijs dat de nulhypothese klopt, maar juist naar bewijs dat de alternatieve hypothese klopt. En, als dat bewijs onvoldoende sterk is, moeten we kunnen terugvallen op een default, dwz de nulhypothese. Hypothesen komen daarom altijd als een setje: \( H_0 \) en \( H_a \)

In principe is het mogelijk om allerlei alternatieve hypothesen op te stellen in een onderzoek. In de praktijk zul je echter meestal één van de volgende drie vormen tegenkomen voor de one-sample t-toets:

• \( H_a: \mu > ....\)
• \( H_a: \mu < ....\)
• \( H_a: \mu ≠ ....\)

, en voor de independent samples t-toets en de gepaarde t-toets neemt dat één van deze drie vormen aan:

• \( H_a: \mu_1 > \mu_2 \)
• \( H_a: \mu_1 < \mu_2 \)
• \( H_a: \mu_1 ≠ \mu_2 \)

Het is niet de vraag welke hypothese je zou moeten nemen als onderzoeker, maar de vraag is voor welke alternatieve hypothese de onderzoeker "bewijs" zou willen vinden. Als de onderzoeker bijvoorbeeld vast wil stellen hoeveel bewijs er is voor wat er in de eerste vorm wordt beweerd, neem dan die hypothese. Waar je precies bewijs voor wil vinden, hangt af van de onderzoeksvraag en de theoretische achtergrond. Bijvoorbeeld, als er sterke theoretische argumenten zijn om te stellen dat een populatiegemiddelde groter is dan... , dan moet je dus niet de hypothese gaan toetsen of het gemiddelde kleiner is want dat lijkt me geen enkele zin te hebben en bovendien sowieso een behoorlijk kansloze onderneming! Kortom, stel vast voor welke stelling/hypothese er bewijs gezocht moet worden, en dat is de alternatieve hypothese.

Als er te weinig bewijs is vóór de alternatieve hypothese, wordt automatisch teruggevallen op de nulhypothese. Gebrek aan bewijs vóór de alternatieve hypothese betekent echter NIET dat er bewijs is tegen de alternatieve hypothese. Het betekent OOK NIET dat er bewijs is vóór de nulhypothese en het betekent ook ZEKER NIET dat er bewijs vóór het tegenovergestelde van de alternatieve hypothese. Dat wil zeggen, gebrek aan bewijs dat het populatiegemiddelde groter is dan ... , wil niet zeggen dat het gelijk is aan ... , en ook niet dat het kleiner is dan .... . Het betekent alleen: gebrek aan bewijs vóór deze alternatieve hypothese, punt uit klaar.

Hoe steekt de bewijsvoering in elkaar?

Zie een hypothesetoets als een soort gedachte-experiment:
Stel, en het hoeft dus niet zo te zijn, maar stel eens dat de nulhypothese juist zou zijn voor de populatie die bestudeerd wordt. Er zouden dan heel veel random steekproeven uit deze populatie kunnen worden genomen. Voor al die steekproeven kan een t-waarde worden berekend met de gebruikelijke formules. Wiskundig kan worden aangetoond dat het histogram van deze t-waarden een Student (T-)verdeling zal zijn als de meetwaarden Normaal waren verdeeld, en sterk zal lijken op een Student (T-)verdeling als dat niet zo was (dit wordt beter met grotere steekproeven).

Deze verdeling is een kansverdeling waarin in principe kan worden opgezocht hoe vaak een t-waarde in een bepaald interval valt, of groter, of kleiner zou zijn dan een of andere waarde. Let wel, dit is een kansverdeling die er van uitgaat dat de nulhypothese waar is!

Voor de steekproef die daadwerkelijk werd gemeten, kan ook een t-waarde worden bepaald. Met behulp van de theoretische kansverdeling, kan bepaald worden wat de kans was om die t-waarde te vinden of hoger, als \( H_0 \) waar zou zijn geweest. Er kan ook gekeken worden wat de kans was om de gevonden t-waarde of kleiner te vinden, als \( H_0 \) waar geweest zou zijn. En er zou ook gekeken kunnen worden naar wat de kans was om een t-waarde te vinden die verder weg lag van 0, dan gevonden is.

Stel nu eens dat we de volgende set van nul- en alternatieve hypothese hebben in een one-sample t-test:

\( \left\{ \begin{array}{1} H_0: \mu = 100 \\ H_a: \mu > 100 \end{array} \right. \)

In de steekproef werd gevonden dat het steekproefgemiddelde 110 is. Omdat het steekproefgemiddelde groter is dan wat er in de nulhypothese staat, zal de t-waarde positief zijn.

Het eerste goede nieuws is dat dit steekproefgemiddelde in elk geval al in de goede richting wijst, want het steekproefgemiddelde was immers groter dan 100. Een steekproefgemiddelde dat kleiner dan 100 was, zou toch lastig aan te voeren zijn als bewijs dat het populatiegemiddelde groter is dan 100, niet waar? Goed, er is dus al een beetje bewijs voor de alternatieve hypothese, maar dat is nog niet overtuigend genoeg.

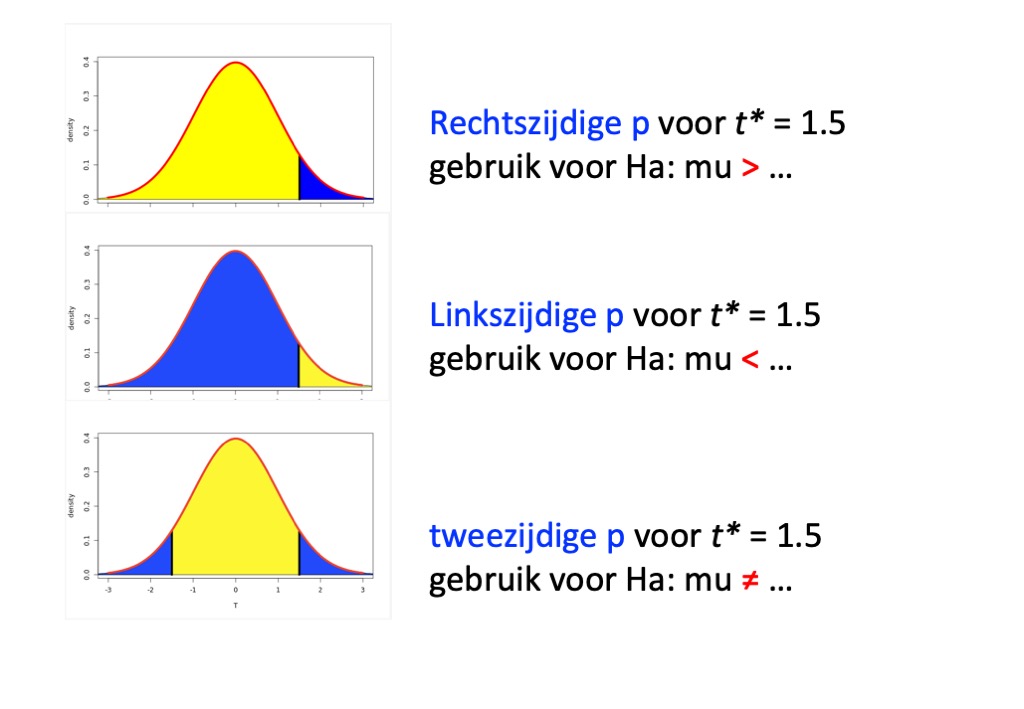
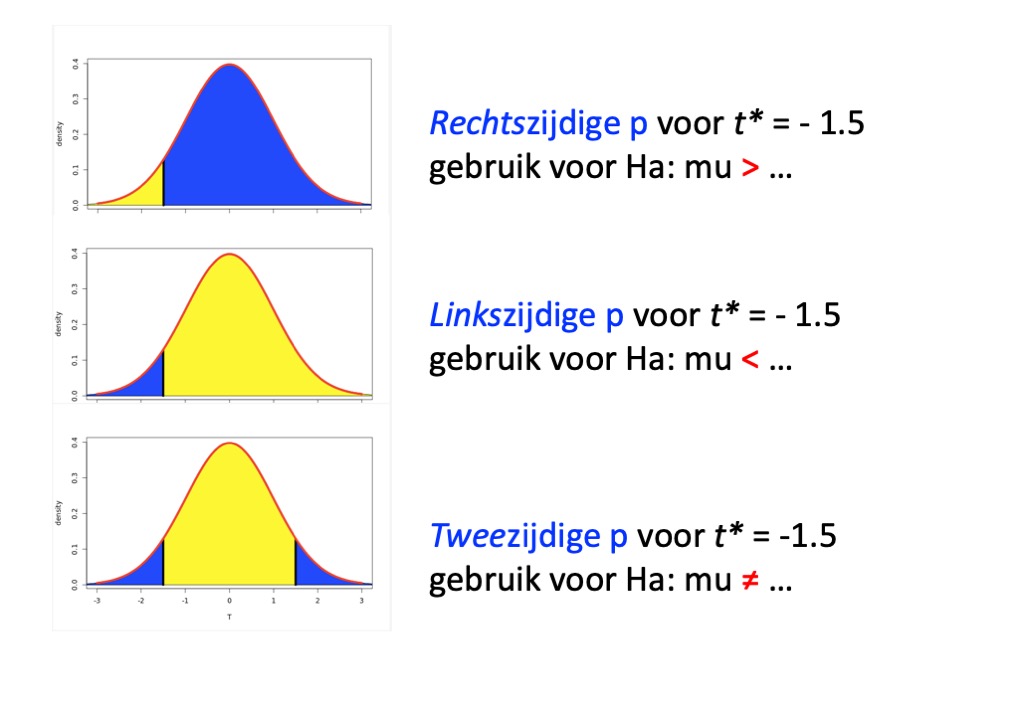
Hoe verder het steekproefgemiddelde boven 100 ligt (en dus ook hoe groter de t-waarde is) des te meer evidentie is er dat deze alternatieve hypothese klopt. Steekproefgemiddelden die zo groot zijn dat ze eigenlijk niet voor kunnen komen als H0 waar is, vormen zelfs een sterk bewijs dat Ha klopt. Met andere woorden, als de kans om de gevonden t-waarde of hoger te vinden als H0 waar zou zijn, heel klein is, is dat bewijs vóór de alternatieve hypothese \(H_a: \mu > ... \). In andere woorden het populatiegemiddelde moet wel groter zijn, zoals in de alternatieve hypothese wordt gesteld, want anders had er eigenlijk niet een steekproef met zo'n hoog gemiddelde uit de populatie voort kunnen komen. Met een hoger populatiegemiddelde zou er wel een redelijkere kans geweest zijn op deze steekproef". In een Student(t-)verdeling is de kans op deze t-waarde of groter het deel van de kansverdeling dat rechts van de gevonden t-waarde ligt. Zie Figuren 1a en 2a voor respectievelijk de situatie dat de t-waarde positief of negatief. In beide gevallen is het het deel van de verdeling rechts van de t-waarde. Dit is de rechtszijdige overschrijdingskans (aka rechtszijdige p-waarde) en voor deze t-waarde die hoort bij de alternatieve hypothese in de vorm van \(H_a: \mu > ... \).

De voorgaande redenering kan ook omgedraaid worden: Bewijs voor de alternatieve hypothese \(H_a: \mu < ... \), wordt dan gevormd door de kans om de gevonden t-waarde te vinden of kleiner, als H0 waar zou zijn. In een Student(t-)verdeling is dat het deel van de kansverdeling dat links van de gevonden t-waarde ligt. Dit is de linkszijdige overschrijdingskans (aka linkszijdige p-waarde)en die hoort bij de alternatieve hypothese in de vorm van \(H_a: \mu < ... \) . Zie Figuren 1b en 2b voor respectievelijk een positieve en negatieve t-waarde. Voor elke t-waarde geldt altijd dat de rechtszijdige p-waarde voor die t-waarde + de linkszijdige p-waarde voor die zelfde t-waarde gelijk is aan 1.

Er is nog een derde vorm voor de alternatieve hypothese, namelijk: \(H_a: \mu ≠ ... \) . Om support te vinden vóór deze specifieke alternatieve hypothese zou er gekeken moeten worden naar de kans om een t-waarde te vinden die groter òf kleiner is dan wat er daadwerkelijk in de steekproef is gevonden. Grote positieve of grote negatieve t-waardes, wijzen er op dat H0 niet kan kloppen omdat die populatie maar zeer zelden zo'n grote t- waarde had opgeleverd. Dit is het deel van de kansverdeling dat rechts ligt van de (positief gemaakte) t-waarde plus het deel wat links van de (negatief gemaakte) t-waarde ligt. Zie Figuren 1c en 2c. In dit geval maakt het dus niet uit of t negatief of positef is; zowel een negatieve en een positieve t-waarde (van dezelfde grootte) geven dezelfde tweezijdige p-waarde. Omdat deze kansverdeling symmetrisch is, wordt ook wel gezegd dat de tweezijdige p-waarde gelijk is aan 2x het deel wat rechts ligt van de positief gemaakt t-waarde. Dit is de tweezijdige p-waarde en die hoort bij de alternatieve hypothese in de vorm van \( H_a: \mu ≠ ... \) .

Een hardnekkig misverstand dat we in de praktijk vaak zien, is dat de éénzijdige p-waarde de helft is van de tweezijdige p-waarde en dat dus de tweezijdige p-waarde twee maal zo groot is als de éénzijdige p-waarde. Dit is simpelweg niet juist. Het maakt namelijk uit of het gaat om de links- of rechtszijdige p-waarde. Neem bijvoorbeeld de volgende situatie: Er is een t-waarde gevonden van 2.1. Met 100 vrijheidsgraden zal dat een tweezijdige p-waarde geven van 0.0382. De rechtszijdige p-waarde die hoort bij t=2.1, is 0.0191 wat inderdaad de helft is, maar de linkszijdige p-waarde is toch echt "het deel van de verdeling dat links van t=2.1 ligt" en dat is 0.9809 en dat is helemaal niet de helft, maar: 1 - ("tweezijdige p" / 2).
Om van een éénzijdige p-waarde naar een tweezijdige p-waarde te gaan, kan wel, maar neem dan de kleinste van de links- en rechtzijdige p-waardes en vermenigvuldig die met 2.

Oneway anova

Een anova wordt gebruikt om "bewijs" te verzamelen dat niet alle groepsgemiddelden in de populatie gelijk zijn. Meestal hebben we dan te maken met meer dan twee groepen (hoewel een anova ook met twee groepen kan worden gedaan). De anova is gebaseerd op de gedachte dat als de groepsgemiddelden in de steekproef veel verder uit elkaar liggen dan mag worden verwacht op basis van de spreiding van meetwaarden binnen de groepen, als er in de populatie inderdaad verschillen in groepsgemiddelden bestaan. De verhouding tussen wat er daardwerkelijk aan verschillen tussen groepsgemiddelden in de steekproef wordt gevonden en wat er verwacht wordt, is de F-waarde.

Bij een F van 1 liggen de groepsgemiddelden in de steekproef precies zover uit elkaar als verwacht zou mogen worden op basis van de verschillen tussen metingen. Hoge F waardes zijn echter een indicatie dat de alternatieve hypothese klopt. F-waardes die kleiner zijn dan 1, zeggen dat de groepsgemiddelden dichter bij elkaar liggen dan verwacht en vormen dus géén indicatie voor groepsverschillen in de populatie. Gelijk aan wat er ook de T-toets wordt gedaan, kan er een kansverdeling worden gemaakt voor de F-waarde als \( H_0 \) waar zou zijn. De p-waarde in deze toets is de kans om een bepaalde F te vinden (of hoger) in de steekproef als H0 waar is. Bewijs vóór de alternatieve hypothese dat niet alle groepsgemidelden gelijk zijn, wordt dus gevonden in de kansverdeling rechts van de gevonden F-waarde.

Omdat in een anova niet getoetst kan worden of het ene gemiddelde groter is dan de andere, maar alleen of de gemiddelden verschillen, wordt er in deze toets niet gesproken over één- of tweezijdig toetsen. De p-waarde is echter wel het "deel van de F-verdeling rechts van de gevonden F-waarde" en dat wordt alleen "p-waarde" genoemd.

T-tabellen en calculators

Veel tabellenboeken waarin bij een t-waarde een p-waarde kan worden opgezocht, geven alleen rechtszijdige p-waardes voor positieve t-waardes. Negatieve t-waardes kunnen echter wel gewoon voorkomen in onderzoek en vaak wordt er ook gevraagd naar linkszijdige p-waardes. Er is een beetje handigheid voor nodig om dergelijke p-waardes in dergelijke tabellen toch te kunnen opzoeken. Als er in het onderzoek een positieve t-waarde is gevonden, kan de rechtszijdige p-waarde direct worden opgezocht. De linkszijdige p-waarde is altijd: 1 - de rechtszijdige p-waarde, zo ook hier dus. De tweezijdige p-waarde is 2x de rechtszijdige p-waarde in deze tabel.

Als er een negatieve p-waarde is gevonden in het onderzoek is de p-waarde wat lastiger en moet je gebruik maken van het feit dat de T-verdeling symmetrisch is. Bijvoorbeeld als de t-waarde -2.1 is, dan moet er bedacht worden dat het deel links van t=- 2.1, gelijk is aan het deel rechts van t=+2.1, en die laatste is wel op te zoeken. De linkszijdige p-waarde van een negatieve t, is dus gelijk aan de rechtszijdige p-waarde van dezelfde t als die positief zou zijn geweest. Bij negatieve t-waarden dus even goed nadenken, of.... een van-t-naar-p calculator gebruiken die voor alle negatieve en positieve t-waardes zowel de links-, rechts- als tweezijdige p-waarde kan bepalen en netjes in een figuurtje uittekent.

Software zoals SPSS geeft voor een t-toets in de regel een tweezijdige p-waarde, omdat het geen weet heeft van welke éénzijdige hypothese er wordt getoetst. In de meest recente versie van SPSS wordt overigens wel een eenzijdige p-waarde gerapporteerd, maar er niet bijgezegd om welke eenzijdige p-waarde het dan gaat! Voorzichtig dus en als je éénzijdig (links dan wel rechts) wil toetsen, zul je de p-waarde zelf hoogstwaarschijnlijk naar de juiste éénzijdige waarde moeten omrekenen.